One-point perspective

To build from the ground up, imagine a frog looking at an extremely ("infinitely") tall sequoia trees. So tall in fact, that in order to see the very tip, the frog must look straight up – at the zenith. Because all the trees extend indefinitely, whichever trunk the frog follows, his gaze ends up in the same direction. It is as if the tree-lines met in a single point. This is the first indication of the existence of a special point that governs the perspective.

The frog's line of sight extends from his eye (the other eye resting closed for the moment) into the three-dimensional world he sees, but it becomes a single point in the two-dimensional perceived image, indicating just the direction of the gaze. And even though the frog's head is stationary, he can look at various parts of the image, by minute eye movements, without altering the whole picture. Most importantly, the trees will still appear to converge to a single point, regardless of whether the frog is currently looking at it.

conifer trees converging to a point as viewed from the frog perspectiveconifer trees slanting due to being seen from the frog perspective

Suppose now, that there are evenly spaced, horizontal branches on each of the trees. The frog knows the branches grow exactly sixty frog-feet apart, but they seem to be growing closer and closer together, the higher he looks. This must be so, for the tree is infinite in length, and there are infinitely many branches which somehow all fit into his field of view. Put another way, if he painted what he sees, the canvas would have finite width and height, and he could not fit infinitely many ievenly spaced branches on it.

Similarly, each branch appears shorter than the one below it. It makes sense that all directions are shrunk, as things get farther away, and yet the vertical direction is distinguished, because of the convergence. After a minute of thought, the frog decides that the tips of the branches form a line themselves. This line, being vertical, approaches the line of the trunk, so the lengths of the branches must decrease. It's all caused by the special point above! he concludes. There really are two effects at play here:

  1. The perceived distance between the trees and the length of the branches both getting shorter as the frog looks higher and higher.
  2. The perceived distance between consecutive branches getting shorter.
The former involves a convergence, and possibly intersection, of all the ideal lines corresponding to the trees. That will be the common perspective point. But the latter is observable already for a single tree, it must be a one-dimensional effect – there is no convergence of lines involved, and no intersection point. We shall come back to this point later on.

For now, the frog decides to return home to his pond, and practice with the one-point perspective.

  • Draw main lines with the left mouse button.
  • Holding 'x' makes the line snap to the perspective direction.
  • Right click to place a perspective line through the mouse pointer and 'X'.
  • Hold the right button to drag a perspective line.





Two-point perspective

When the frog looks right, he discovers a regularity to how the branches are arranged. The ideal trees have perfectly straight branches which, like minature trees lying on their side, all point to the right. And although they are finite in length, they could be imagined to lie on infinite lines which again meet in a common point, perhaps far on the horizon. That the lines should meet at all is again a consequence of the perceived shrinking: The distances between branches look shorter and shorte, as the frog looks farther and farther down the line of trees.

  • Draw main lines with the left mouse button.
  • Holding 'x' or 'y' makes the line snap to the perspective direction 'X' or 'Y', respectively.
  • Right click while holding 'x' or 'y' to place a perspective line through the mouse pointer and the appropriate point.
  • Hold the right button to drag a perspective line, before placing it.





Interlude: Distance

We wonder at this point: do the y-lines help us determine how objects shrink when we look along x-lines? And vice-versa: each tree grows along a vertical line, determined by the point X, but what determines the width of each tree-trunk as we go along the horizontal line? Is there some special spacing along the perspective lines? Perhaps the angles between them?

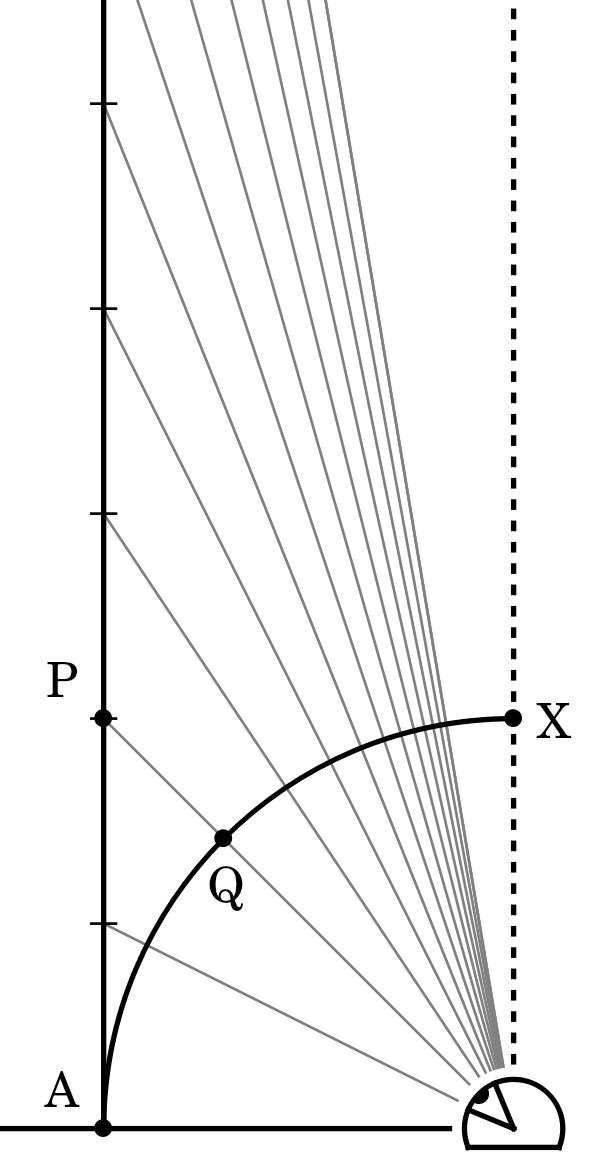
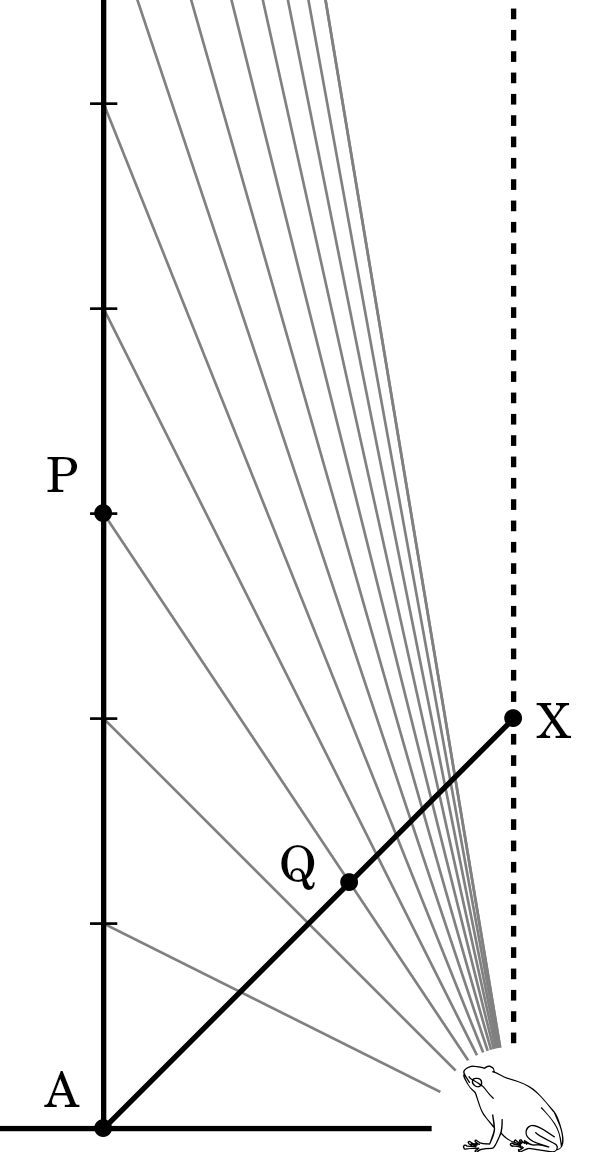
To answer, the frog has to imagine himself from the side, looking at just one tree. As noted before this effect is truly one-dimensional, so one line should be enough. We can depict what he sees in two ways, depending on the model of his internal image. One is spherical, the other flat.

a diagram showing how equal disances are distorted when projected on a sphere around the eye a diagram showing how equal distances are distorted when projected on a plane in front of the eye

These are the two simplest versions of how the actual section of equal distance get projected onto the perceived image, or a canvas. To distill the essential geometry, the frog has been temporarily moved to Flatland, so his field of view encompasses only the arc \(\mathrm{AX}\) (or the segment \(\mathrm{AX}\) in the second version). Either of the lines \(\mathrm{AX}\) constitute everything the frogg can see without moving his eyes, and lengths along \(\mathrm{AX}\) correspond directly to whether an object appears long or short.

And it is not hard to conenct this with the usual two-dimensional field of view that we experience – just imagine, that we are looking at the frog from the side, seeing his canvas \(\mathrm{AX}\) edge-on. But the point is that even in one dimension, the persepctive point X produces progressive shrinking, even before convergence, because it requires an additional dimension along which other trees can grow.

How fast exactly do object shrink? Some basic geometry tell us, that in the first case, the distance along the trunk is just the tangent: \(\mathrm{AP} = \tan(\angle\mathrm{A𓆏Q})\), or, taking the total length of the arc \(\mathrm{AX}\) to be 1: \(\mathrm{AP}=\tan\!\left( \frac{\pi}{2}\mathrm{AQ}\right)\). In the second case the formula can be obtained without trigonometry, just similarity of triangles gives \(\mathrm{AP} = \frac{\mathrm{AQ}}{1-\mathrm{AQ}}\), again assuming that \(\mathrm{AX}\) is of unit length. 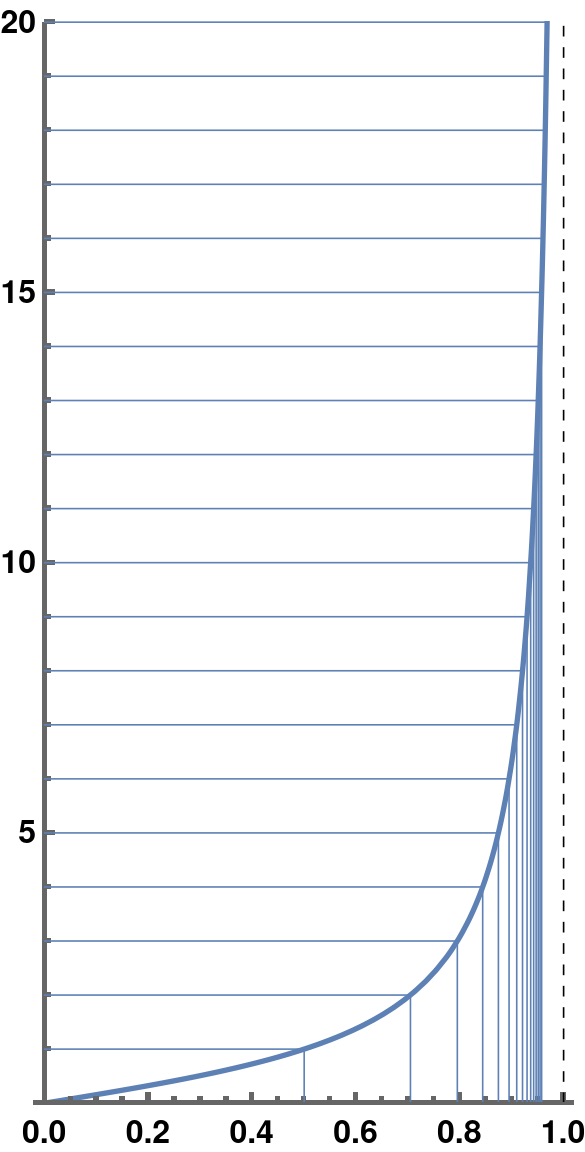Here is what the functions look like.

a graph of the tangent function, describing the spherical distortion a graph comparing the distortions of the spherical and planar cases

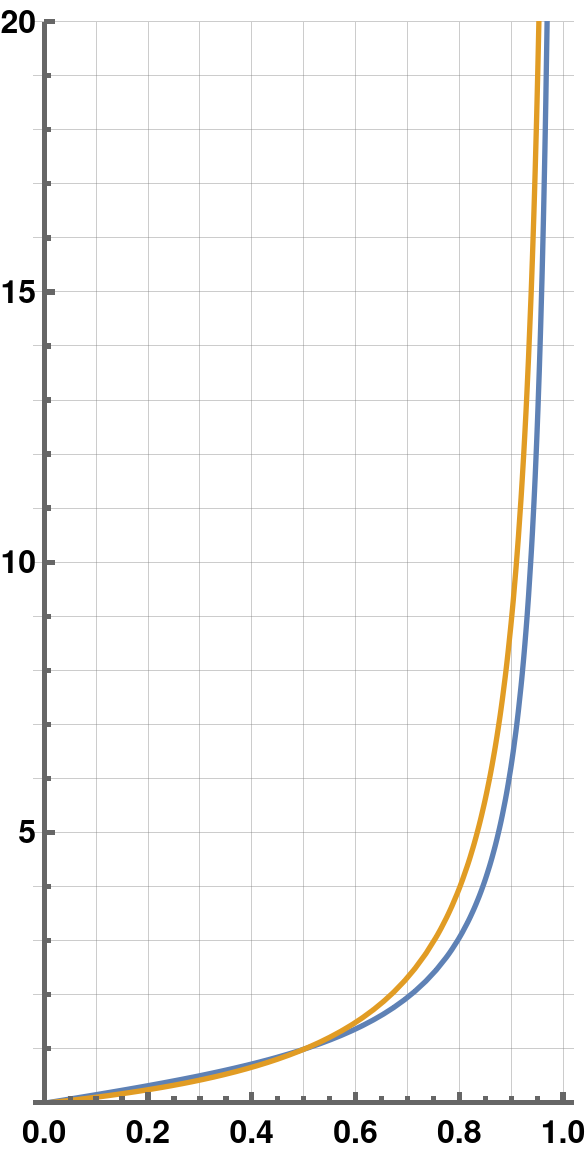
The vertical axis is the tree with real distances on it – these are the spacings between branches. The horizontal axis would, in fact, be the perspective line on the canvas. And the blue vertical lines show how the branches have to be squeezed. The second graph just shows the difference between the spherical and flat version. On a real painting, with details and colours drawing out attention away from the ideal geometry, this difference will be negligible. Especially if the object being painted are not composed of straight lines or artistic liberty is used for emphasis.

Three-point Perspective

Finally!

  • Draw main lines with the left mouse button.
  • Holding 'x' or 'y' makes the line snap to the perspective direction 'X' or 'Y', respectively.
  • Right click while holding 'x' or 'y' to place a perspective line through the mouse pointer and the appropriate point.
  • Hold the right button to drag a perspective line, before placing it.
  • Hold CTRL to select a line with left click.






Conjugate Two-point Perspective

The owl, however, disagrees. When she flies high up by trees, so high that she can no longer see the ground, the trunks appear to extend indefinitely both upward and downward. Not only do the lines converge in the zenith – they do so in the nadir as well. So if the trunks appear thinner and thinner above and below the owl, that means they are the thickest directly in front of her...

  • Draw main lines with the left mouse button.
  • Holding 'x' makes the line bend to the perspective arc between 'XN and 'XS'.
  • Right click while holding 'x' to place a perspective arc through the mouse pointer.
  • Hold the right button to drag a perspective arc, before placing it.
  • Hold CTRL and left click to select a line or arc.






Interlude: Distortion

What about the fish?

A five-point perspective mix

What about the wolf?

Six-point perspective

The passing from a single converging perspective point X to the pair XN and XS corresponds to including both ends of the infinite parallel lines, however paradoxical it may sound. For every such line, the gaze can follow it to infinity forwards or backwards – or left or right, upwards or downwards, as the case may be. There are two distinct directions at which the gaze can end up, and thus two distinct points of convergence.

In three dimensions, there can be, not surprisingly, three mutually perpendicular axes. With each axis comes a pair of such convergence points, so six points in total – exactly like the six faces of a cube.

How the sets of lines bend and converge can best be seen, when they are projected onto an imagined sphere around an all-seeing eye. The vertical lines become the meridians, and likewise for the other directions after some head tilting.

In addition to the cubic room, another Platonic solid applies here: points should more appropriately become corners, not walls, and an octahedron emerges.

  • Draw main lines with the left mouse button.
  • Holding 'x' makes the line bend to the perspective arc between 'XN and 'XS'; and likewise for 'y' and 'z'.
  • Right click while holding 'x', 'y' or 'z' to place a perspective arc through the mouse pointer.
  • Hold the right button to drag a perspective arc, before placing it.
  • Hold CTRL and left click to select a line or arc.






Seven... wait, what?